Many investigators have suggested that strong correlations between the outcomes of modeling (e.g., adjustments in cortical thickness or moments of inertia) remodeling (e.g., increased porosity or osteon density; reduced mineral content) reflect their synergism/ compensation in affecting local or whole-bone performance (Beck et al., 2000, van der Meulen et al., 2001, Ural and Vashishth, 2006, Tommasini et al., 2005, Lazenby, 1986, Burr et al., 1990). For simplicity, compensation is considered here to be a form of synergism. However, synergism/compensation between modeling and remodeling in cortical bone is not well supported. (This does not refer to metaphyseal/epiphyseal regions where overall structural strength might be achieved by synergism/compensation in the relative amounts of cortical and cancellous bone mass.) For example, in a study of osteon population density and cortical thickness in the distal aspect of the mid-third diaphyses of 27 adult human tibiae (age range: 21-87), Ural and Vashishth (2006) showed that these parameters were negatively correlated. This led to their statement that: “…the change in bone microstructure and geometry interact with each other at certain sites and determine the overall mechanical properties and bone fracture” (page 1497). Ural and Vashishth (2006), however, did not find a similar relationship between osteon density and cortical thickness in the proximal aspect of the mid-third diaphysis of the same tibiae. They suggested that these site-specific differences are associated with differences in strain magnitudes and distributions in addition to regional differences in muscle attachments. These suggestions invoke two important considerations that potentially point to what distinguishes the load histories of these nearby regions: (1) the “Load-Complexity Category” (see separate section of the website that deals specifically with this), and (2) the degree of local “Muscle, Tendon, Ligament Protection/Influence” (Table 1).
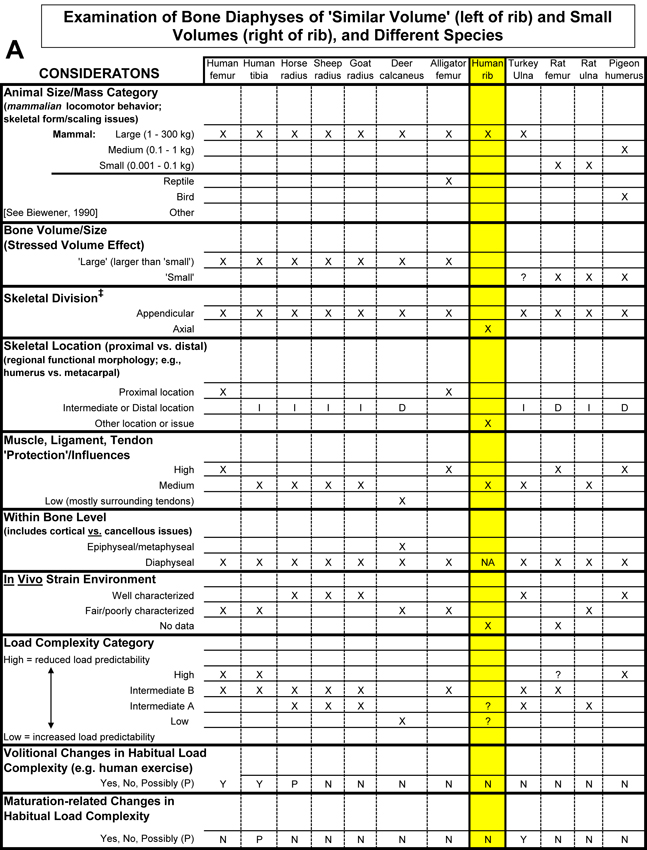
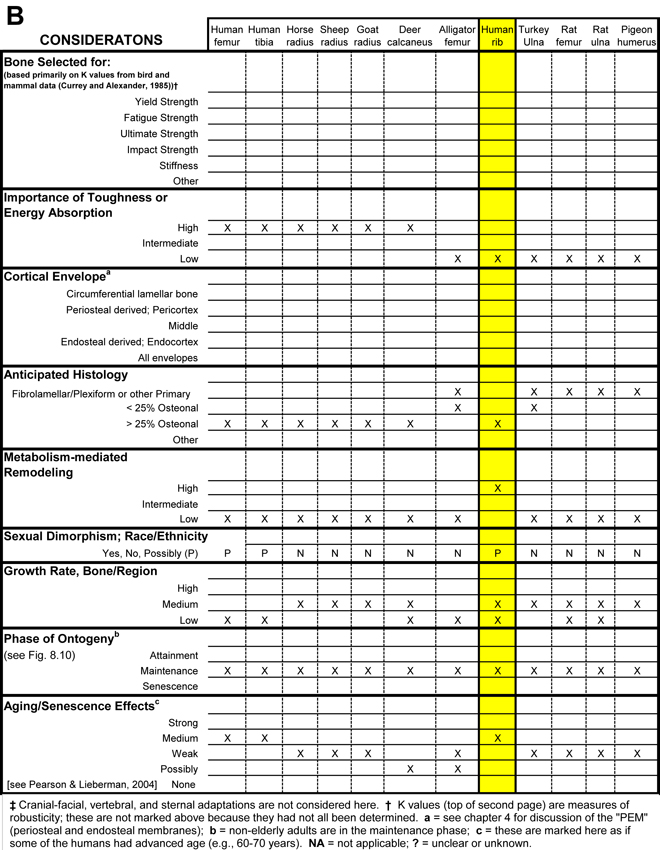
Table 1. Worksheet/checklist of important considerations for interpreting adaptation in the appendicular skeleton.
Another example of putative modeling-remodeling (structural-material) synergism/compensation has been suggested by Drapeau and Streeter (2006) in their study of cross-sectional geometry and osteon population densities in the mid-diaphyseal locations of 18 matched pairs of adult human tibiae and femora (age range: 18-50 years). In the tibiae, they found significant correlations between osteon population densities and axes of cross-sectional moments of inertia (Imax, Imin; defined in the section on Bone Biomechanics). The authors were puzzled by the absence of a similar relationship in the femoral diaphyses. As discussed further below, the basis of this expectation is further confounded by the fact that these bones are in different load-complexity categories.
Lazenby (1986) also felt that structural-material synergism/compensation was detected in a sample of 13 adult human femora (age range:50-96; one bone from an 80 year-old individual was omitted from the statistical analysis). Lazenby reported a significant inverse relationship between the magnitude of the axes of the cross-sectional moment of inertia and porosity, with the presumed common objective of ‘adjusting the bone’s bending rigidity’. In other words, greater porosity was found in the direction of maximum bending resistance indicating that ‘‘weaker’’ material properties from greater porosity were coupled with ‘‘stronger’’ bending resistance from cortical bone geometry. In addition, the porosity difference along the Imax and Imin axes appeared to decline as the geometrical difference between Imax and Imin declined, indicating that the porosity became more evenly distributed as the bone’s cross-section and distribution of mass became more circular/symmetrical (r = -0.56; p = 0.05). In addition to the fact that this relationship has not been independently corroborated (e.g., (Drapeau and Streeter, 2006)), this study appears to be subject to insufficient statistical power. This is due to the small sample size and selection bias because, as noted, one of the 13 femora was excluded due to greater porosity along its Imax when the other 12 had greater porosity along their Imin. When all 13 femora are included, there is no correlation between the rigidity ratio and the porosity ratio (r = -0.06, p > 0.8); thus demonstrating no relationship between porosity distribution and cortical bone distribution as defined by Imax and Imin — rejecting the hypothesis of synergism/compensation between modeling and remodeling.
Putative examples of modeling-remodeling synergism expressed in terms of ‘regional’ safety factors in diaphyseal cortices have also been refuted. For adequate structural performance a bone must have adequate safety factors. A bone’s safety factor refers to the ratio of yield stress (or strain) to peak physiological stress (or strain), and represents a means of quantifying how strong the bone is in relation to how strong it needs to be to avoid fracture (safety factor = yield or ultimate stress / peak physiological stress).
Safety factors, when considered in skeletal biomechanics, usually refer to an entire bone (Rubin and Lanyon, 1982, Biewener, 1993). The idea of ‘regional’ safety factors (i.e., those from a distinct cortical location within the same transverse cross section) has also been considered in studies of the goals of bone adaptation (Riggs et al., 1993, Lanyon et al., 1979, Skedros et al., 1994). Indeed, in these studies it was hypothesized that a major objective of correlated structural and material characteristics (e.g., inverse relationship of cortical thickness and mineralization) in limb-bone diaphyses exhibited by some bones is the achievement of uniform regional safety factors between discrete cortical locations (e.g. between anterior and posterior cortices at mid-diaphysis). This hypothesis is a poignant example of putative synergism between the modeling and remodeling processes.
As attractive as the hypothesis of unifying regional safety factors between discrete cortical locations may seem, this synergism has not been supported in our studies of equine third metacarpals (Skedros et al., 2003). Readers who seek more in-depth understanding of this topic are referred to this study. These results provide the impetus for challenging the idea of close synergism/compensation between structure (modeling) and material (remodeling). It is possible that some form of synergism/compensation might exist if safety factors are defined in terms of energy absorption and/or fatigue resistance (Joo et al., 2007). Studies that explore this possibility are needed.
References
Beck TJ, Looker AC, Ruff CB, Sievanen H, Wahner HW (2000) Structural trends in the aging femoral neck and proximal shaft: Analysis of the Third National Health and Nutrition Examination Survey dual-energy X-ray absorptiometry data. J Bone Miner Res, 15, 2297-304.
Biewener AA (1993) Safety factors in bone strength. Calcif. Tissue. Int., 53, S68-S74.
Burr DB, Ruff CB, Thompson DD (1990) Patterns of skeletal histologic change through time: Comparison of an archaic native American population with modern populations. The Anat. Rec., 226, 307-313.
Drapeau MS, Streeter MA (2006) Modeling and remodeling responses to normal loading in the human lower limb. Am J Phys Anthropol, 129, 403-9.
Joo W, Jepsen KJ, Davy DT (2007) The effect of recovery time and test conditions on viscoelastic measures of tensile damage in cortical bone. J Biomech, 40, 2731-7.
Lanyon LE, Magee PT, Baggott DG (1979) The relationship of functional stress and strain to the processes of bone remodeling: An experimental study on the sheep radius. J. Biomech., 12, 593-600.
Lazenby R (1986) Porosity-geometry interaction in the conversation of bone strength. J Biomech, 19, 257-8.
Riggs CM, Vaughan LE, Boyde A, Lanyon LE (1993) Mechanical implications of collagen fibre orientation in cortical bone of the equine radius. Anat Embryol, 187, 239-248.
Rubin CT, Lanyon LE (1982) Limb mechanics as a function of speed and gait: A study of functional strains in the radius and tibia of horse and dog. J Exp Biol, 101, 187-211.
Skedros JG, Bloebaum RD, Mason MW, Bramble DM (1994) Analysis of a tension/compression skeletal system: Possible strain-specific differences in the hierarchical organization of bone. Anat Rec, 239, 396-404.
Skedros JG, Dayton MR, Sybrowsky CL, Bloebaum RD, Bachus KN (2003) Are uniform regional safety factors an objective of adaptive modeling/remodeling in cortical bone? J Exp Biol, 206, 2431-2439.
Tommasini SM, Nasser P, Schaffler MB, Jepsen KJ (2005) Relationship between bone morphology and bone quality in male tibias: implications for stress fracture risk. J Bone Miner Res, 20, 1372-80.
Ural A, Vashishth D (2006) Interactions between microstructural and geometrical adaptation in human cortical bone. J Orthop Res, 24, 1489-98.
van der Meulen MC, Jepsen KJ, Mikic B (2001) Understanding bone strength: Size isn’t everything. Bone, 29, 101-104.